Matemática
e suas Tecnologias
Livro do Estudante
Ensino Médio
A Matemática: uma
construção da humanidade
A Matemática e o dia-a-dia
As condições de vida da humanidade se
modificaram ao longo do tempo, com o
desenvolvimento da agricultura, do comércio, da
indústria, do conhecimento e da tecnologia . E
através das conseqüências do avanço em todas
essas áreas.
Apesar de o homem não ter registrado o que fazia
e pensava no início de sua história, ele precisava
resolver problemas de seu dia-a-dia, ligados à sua
subsistência.
Ao buscar soluções para eles, o conhecimento
matemático começou a ser construído.
A Matemática e a linguagem
Tanto o pescador como o caçador pensaram de
um modo até bastante sofisticado. Entretanto,
talvez a estratégia que utilizaram para resolver
a questão da troca já não fosse tão eficiente se
tivessem que decidir quantos peixes trocar por
560 aves!
Com o correr do tempo, o homem passou a
produzir mais e a ter um estoque do que
produzia (superávit), além da necessidade do
consumo próprio e de seu grupo. Com isso, as
idéias e técnicas matemáticas foram se
aperfeiçoando, para poder resolver os
problemas que envolviam grandes
quantidades, por exemplo.
É bem possível que você tenha resolvido o
problema dos peixes de um modo mais rápido,
como por exemplo:
Esses símbolos que atualmente combinamos e
usamos de um modo conveniente para registrar a
resolução do problema dos peixes fazem parte de
uma linguagem escrita que foi sendo construída,
à medida que as idéias e conceitos matemáticos
foram sendo descobertos, elaborados e aplicados
pelo homem em outras situações: é a linguagem
matemática.
Essa linguagem, quando é escrita, utiliza símbolos
próprios e universais, o que permite uma
comunicação que ultrapassa fronteiras das
diversas línguas. Entretanto, quando nos
comunicamos oralmente, utilizando essa
linguagem, lançamos mão da língua materna.
Veja um exemplo:
Um freguês de uma padaria compra,
todos os dias, leite a R$1,10 o litro e
alguns pãezinhos a R$ 0,20 cada. Como
se pode representar a despesa dessa
pessoa num dia?
A situação acima, descrita em nossa língua
materna, pode ser registrada por meio da
linguagem matemática, que favorece a
representação da despesa desse freguês para
qualquer quantidade de pães que ele compre.
Podemos representar por n o número de pães e
por f(n) (lê-se “f de n”) a despesa. Assim, a
despesa pode ser representada pela igualdade:
f (n) = 1,10 + 0,20 . n
Despesa
total
Despesa
com o leite
Despesa
com os pães
Figura 3
11 . 3 = 33
ou
22 2
00 11
2
3
22
x =
então x = = 33 3 . 22
2
Matemática e suas Tecnologias Ensino Médio
14
2
3
Desenvolvendo competências
Você e as placas de trânsito
Algumas placas de trânsito que você
encontra nas ruas e estradas utilizam uma
“linguagem” simbólica, muitas vezes
impregnada de idéias matemáticas.
Observe as placas ao lado.
a) O que elas significam?
b) Que idéia matemática cada uma delas
utiliza?
A todo momento, podemos constatar nos meios
de comunicação (televisão, jornais, revistas,
internet, folhetos, livros etc.), a presença dessa
“linguagem”. Uma pessoa que não a domina, não é
Pense um pouco sobre os gráficos acima:
Os gráficos publicados pelo jornal fizeram parte de
matéria sobre o “caso cracolândia”, ocorrido na
capaz de compreender as informações apresentadas,
o que poderá torná-la incapaz de participar de
maneira integral de uma vida em sociedade cidade de São Paulo, no final de 2001, e dizem
respeito às ações promovidas pela Corregedoria da
polícia civil e à situação de seus funcionários.
Você já viu que o desenvolvimento da Matemática
se deve em grande parte à busca de soluções para
problemas que a humanidade tem enfrentado em
seu dia-a-dia. Apenas para dar alguns exemplos:
• Que chance tenho em ter meu bilhete sorteado
numa loteria de números?
• Como fixar as ripas de meu portão?
• Quantas estampas diferentes posso obter nos
tecidos da tecelagem onde trabalho, se o fundo
pode ser ou azul ou amarelo e o desenho pode
ser de bolinhas brancas ou de listras pretas ou,
ainda, xadrez vermelho?
Questões semelhantes a essa fizeram o homem
pensar nos fenômenos probabilísticos, em
questões geométricas, e nos problemas de
contagem, respectivamente. Além desses campos
específicos da Matemática aos quais eles se
referem, outros mais foram desenvolvidos a partir
de problemas que envolviam números, medidas,
álgebra, ligados à realidade da humanidade.
Entretanto, os outros campos do conhecimento
também têm solicitado respostas da Matemática
para solucionar seus problemas específicos,
contribuindo indiretamente para seu
desenvolvimento.
Para citar um exemplo que mostra a Matemática
sendo utilizada em outro campo do conhecimento,
vamos focalizar nosso olhar na Trigonometria,
ramo da Matemática que, até por volta do século
XVII, desenvolveu-se em decorrência de uma
ligação estreita entre a teoria e a prática.
No início de sua criação, a Trigonometria era
um campo da Matemática no qual os ângulos de
um triângulo e as medidas de seus lados eram
relacionados.
As razões trigonométricas apareceram
inicialmente por necessidades da Astronomia,
da Agrimensura e da navegação.
Posteriormente, por volta dos séculos XVI e XVII,
a Trigonometria esteve a serviço da Física para
descrever e explicar fenômenos periódicos, como
por exemplo:
• o movimento periódico dos planetas, estudado
por Kepler.
• o movimento periódico dos pêndulos, estudado
por Galileu.
• a propagação do som em forma de ondas,
estudada por Newton.
• a propagação da luz em forma de ondas,
estudada por Huyghens.
• a vibração de uma corda de violino, estudada
por Mersenne.
Razões Trigonométricas
As razões trigonométricas já eram utilizadas pelos
egípcios para resolver problemas de Arquitetura,
por ocasião das construções das pirâmides. Para
manter constante a inclinação das paredes das
pirâmides durante a construção, eles mantinham
constante o quociente do “afastamento
horizontal” pelo “afastamento vertical”, que eram
medidos com unidades diferentes.
Já no final do século XVII, com o início do
desenvolvimento do conceito de Função, o
estudo da Trigonometria se ampliou para um
campo mais abstrato, desligando-se assim das
aplicações práticas.
Figura 6 – Onde a, b e c são as medidas dos catetos
e da hipotenusa desse triângulo retângulo; a e b seus
ângulos agudos; e sen (seno), cos (co-seno) e tg
(tangente) são razões entre medidas dos lados desse
triângulo, como estão descritas acima.
h1 h2 h3
v1 v2 v3
=== ... = c (constante)
As razões trigonométricas já eram utilizadas pelos
egípcios para resolver problemas de Arquitetura,
por ocasião das construções das pirâmides.
Para
manter constante a inclinação das paredes das
pirâmides durante a construção, eles mantinham
constante o quociente do “afastamento
horizontal” pelo “afastamento vertical”, que eram
medidos com unidades diferentes.
Atualmente, as razões trigonométricas num
triângulo retângulo são apresentadas sempre a
mesma inclinação.
Ora, o quociente entre as medidas é nada mais,
nada menos, do que uma razão trigonométrica,
conhecida hoje por cotangente do ângulo de
inclinação da parede com o chão.
Hoje em dia mede-se a inclinação de uma reta por
uma razão entre segmentos verticais e horizontais
(tangente do ângulo de inclinação), razão essa
inversa da utilizada pelos egípcios para
resolverem problemas arquitetônicos.
A Matemática e suas questões internas
Quantas vezes você já deve ter feito a mesma
pergunta que aparece na Figura 18, não é mesmo?
Muitas vezes aprendemos conceitos matemáticos
que, à primeira vista, nada têm a ver com a
realidade em que vivemos. Posteriormente,
percebemos que eles serviram para construirmos
novos conceitos e idéias matemáticas que têm
grande aplicação em nossa vida.
Um exemplo interessante é o dos números
complexos. É muito comum entrarmos em contato
com esse tipo de número por meio de problemas
que envolvem raiz quadrada de número negativo.
Veja um problema famoso a seguir:
Descubra dois números cuja
soma é 10 e cujo produto é 40.
Esse problema foi objeto de estudo do matemático
italiano Cardano, em 1545, que o considerou
“manifestamente impossível, mas mesmo assim
vamos operar”.
A equação do segundo grau já era conhecida no
tempo de Cardano: ax2
+ bx + c = 0 e a fórmula
que a resolve também:
onde a, b e c são números reais.
Cardano concluiu que a equação que resolvia esse
problema é x2
–10 x + 40 = 0 e que
eram soluções do problema. Entretanto considerou
essas expressões inúteis, pois envolviam números
para os quais ainda não tinha sido dado nenhum
significado: a raiz quadrada de número negativo.
Nesse tempo, Bombelli, outro matemático italiano,
resolveu operar com esses números, mesmo sem
dar a eles um significado, imitando o
procedimento que utilizava para operar com
números reais.
Bombelli confirma, por exemplo, que a soma e o
produto dos números e soluções do problema
inicial são 10 e 40, respectivamente. Ele operou
com esses números usando as mesmas regras e
propriedades dos números reais que conhecia.
Usando a Matemática para modificar o mundo
A todo momento convivemos com uma grande
quantidade de objetos, fatos e informações de
procedências e naturezas diversas. Por isso,
precisamos compreendê-los, analisá-los,
relacioná-los e, muitas vezes modificá-los, para
tornar melhor a realidade em que vivemos.
Arrumar os objetos no armário demanda de você
uma habilidade em ocupar o espaço de modo
conveniente para que todos os objetos caibam.
Mas não só isso. É possível que você queira
colocar na prateleira de cima os objetos que usa
para escrever (lápis, caderno e livro) e na de
baixo os que não utiliza para esse fim (relógio,
tesoura, caixinhas). Isso mesmo, você classifica os
objetos de acordo com o critério que mais lhe
interessa.
Já a questão do lixo é mais complexa, pois sua
solução não depende apenas de você! Que tal uma
campanha de conscientização entre as pessoas que
moram no seu quarteirão? Como fazer isso? Seria
bom fazer uma coleta seletiva? As pessoas sabem
o que é isso?
Afinal, o que a Matemática tem a ver com o lixo?
Ora, uma campanha de conscientização sobre a
coleta do lixo pode ser feita com as pessoas que
moram em seu quarteirão. Ela pode ser
desenvolvida em várias etapas, como, por exemplo:
Um grupo de vizinhos interessados em solucionar
o problema pode se organizar para fazer essa
campanha.
Fazer um levantamento:
• do tipo de lixo que é jogado nas ruas
(observando as ruas todos os dias, durante um
certo período estipulado pela equipe,
recolhendo e anotando o lixo encontrado:
papéis, casca de frutas, embalagens, garrafas etc).
Para fazer essa coleta, o grupo de vizinhos deve
se munir de luvas de borracha, sacos de lixo de
20 litros marcados com cores diferentes (azul
Usando a Matemática para modificar o mundo
A todo momento convivemos com uma grande
quantidade de objetos, fatos e informações de
procedências e naturezas diversas. Por isso,
precisamos compreendê-los, analisá-los,
relacioná-los e, muitas vezes modificá-los, para
tornar melhor a realidade em que vivemos.
Você pode notar que essas três situações são de
caráter muito diferente.
Arrumar os objetos no armário demanda de você
uma habilidade em ocupar o espaço de modo
conveniente para que todos os objetos caibam.
Mas não só isso. É possível que você queira
colocar na prateleira de cima os objetos que usa
para escrever (lápis, caderno e livro) e na de
baixo os que não utiliza para esse fim (relógio,
tesoura, caixinhas). Isso mesmo, você classifica os
objetos de acordo com o critério que mais lhe
interessa.
Já a questão do lixo é mais complexa, pois sua
solução não depende apenas de você! Que tal uma
campanha de conscientização entre as pessoas que
moram no seu quarteirão? Como fazer isso? Seria
bom fazer uma coleta seletiva? As pessoas sabem
o que é isso?
Os exemplos são tantos, que tropeçamos neles em
nosso dia-a-dia, desde os mais simples, até os
mais complexos:
Figura 20 Figura 21 Figura 22
Capítulo I — A Matemática: uma construção da humanidade
27
para papel; verde para vidro; amarelo para
latas; vermelho para plásticos; branco para lixo
orgânico).
• de como é feita a coleta de lixo nesse quarteirão
(por caminhão coletor, por cada morador que
queima seu lixo ou leva-o para um depósito
comunitário etc.);
• sobre o conhecimento que as pessoas têm sobre
coleta seletiva e se praticam a coleta seletiva;
Papel
Vidro
Latas de bebida
Orgânico (restos de
alimentos, folhas,
animais mortos etc)
Plástico
2kg
1kg
3kg
3kg
Sarjeta
Portas de casas
Sarjeta, calçadas
Sarjeta, calçadas, rua
porta de casa
Tipo de lixo Quantidade Local
1kg Sarjeta, esquinas
Conhece
Não conhece
10
1
15
64
Coleta seletiva de lixo Pratica Não pratica
papel
34
12
44
vidro
2
0
88
lata
24
15
51
orgânico
13
8
69
plástico
6
10
74
Tipo de lixo
Em relação ao hábito de jogar lixo na rua,
a Tabela 1 apresenta o nº de moradores em cada situação:
Em relação ao conhecimento e à prática da coleta seletiva de lixo,
a Tabela 2 apresenta o nº de moradores em cada situação:
Em relação ao tipo de lixo e à quantidade encontrados nas ruas durante
um certo período (por exemplo, 1 semana):
Tabela 1
Tabela 2
Tabela 3
• sobre os insetos mais freqüentes nas casas desse
quarteirão e na parte externa às moradias;
O grupo de vizinhos poderá encontrar outros
itens que considerar mais convenientes.
De posse desses dados, o grupo poderá arrumá-los
em tabelas, poderá também confeccionar gráficos
para a conscientização dos moradores do
quarteirão.
A elaboração das tabelas favorecerá:
• a observação de semelhanças e diferenças entre
os materiais coletados e, portanto, favorecerá os
processos de classificação para a realização de
coleta seletiva.
• a tabulação e análise de dados. Na coleta
encontrou-se um número muito maior de latas
do que garrafas de vidro. A que se deve esse
fato? Na pesquisa, percebeu-se que o hábito de
jogar papel e latinhas de refrigerante ou cerveja
ainda é muito forte entre os moradores desse
quarteirão. O que se poderia fazer a respeito?
• os cálculos que por ventura devam ser feitos
para, por exemplo, fazer previsões: se cada
garrafa coletada pesa em média 300g e cada lata
50g, quantas garrafas e quantas latas foram
coletadas na semana? Se os sacos de lixo
utilizados na coleta suportam em média 20kg,
de quantos sacos vamos precisar para a próxima
semana de coleta?
• a observação de regularidades. A tabela anterior
mostra que é na sarjeta que se encontra a maior
diversidade de lixo.
• a verificação de quantos moradores estão
envolvidos, direta ou indiretamente, na coleta
de lixo do quarteirão em questão: na primeira
tabela é fácil perceber que são 90 essas pessoas.
• a previsão sobre as medidas que deverão ser
tomadas para conscientizar as pessoas que não
conhecem ou não praticam a coleta seletiva (ao
todo 80 moradores do quarteirão). Essas
medidas podem ser de vários tipos: folhetos
explicativos, reuniões com os moradores do
quarteirão, visitas do grupo de pesquisa a cada
casa do quarteirão para explicar sobre a coleta
de lixo etc.
• a confecção de gráficos que possam, por meio
do impacto visual, mostrar aos moradores do
quarteirão o problema do lixo de forma
imediata. Um cartaz como o seguinte (Figura
23) nos mostra que os moradores do quarteirão
precisam ser informados sobre o que é a coleta
seletiva e suas vantagens.
Para confeccionar um gráfico desse tipo
(gráfico de setores), você precisa mobilizar
conhecimentos sobre:
• ângulo, ângulo central.
• setor circular.
• proporcionalidade (entre ângulo central do setor
e o número de moradores que não conhecem ou
não praticam coleta seletiva do lixo).
Lógica e argumentação:
da prática à Matemática
Argumentação
Você já pensou no que existe em comum entre
uma propaganda de certo produto na televisão,
um artigo do editorial de um jornal e um debate
entre dois políticos? Essas situações podem
parecer bem diferentes, mas, se você analisar com
cuidado, verá que, nos três casos, basicamente,
tenta-se convencer uma ou mais pessoas de
determinada idéia ou teoria.
Os criadores do comercial procuram convencer o
público de que aquele produto é melhor do que o
de seus concorrentes. O jornalista que escreve um
artigo defende seu ponto de vista sobre um
acontecimento do dia anterior e procura
convencer os leitores de que suas idéias são as
mais corretas. Já cada um dos políticos tenta
mostrar aos eleitores que possui melhores
condições de ocupar determinado cargo público
do que seu adversário.
Mas como convencer alguém, ou nós mesmos, de
que determinada idéia é, de fato, correta? É
necessário que sejam apresentados fatos que
justifiquem aquela idéia. Esses fatos são chamados
de argumentos. Eles devem ser bem claros, ter
uma relação lógica entre si, de tal maneira que a
idéia considerada seja uma conseqüência natural
dos argumentos apresentados.
Nem sempre, porém, isso ocorre. Muitas vezes, a
argumentação não é feita de modo consistente e o
resultado é que aquela idéia acaba não sendo
aceita pelas outras pessoas.
O sistema numérico
Muitos séculos se passaram até que os hindus
desenvolvessem o sistema de numeração decimal.
Por não haver muitos documentos sobre a
Matemática conhecida na Antigüidade, é
impossível saber, com exatidão, quando isso
aconteceu. Estima-se ter sido por volta do século
V d.C.
Os algarismos: 0; 1; 2; 3; 4; 5; 6; 7; 8 e 9
escolhidos para compor o sistema de numeração
decimal e posicional foram por muito tempo
denominados erroneamente algarismos arábicos,
por terem sido apresentados pelos árabes. Por
volta do século VII, ao entrarem em contato com a
cultura hindu e motivados pela simplicidade e
praticidade do sistema de numeração encontrado,
tornaram-se seus divulgadores em todo o Oriente.
Assim, mais tarde, esses algarismos passaram a ser
conhecidos como hindu–arábicos.
Em toda a Europa, durante muitos séculos, o
sistema numérico usado era o romano e, apesar da
simplicidade do sistema hindu-arábico, houve
muita resistência à sua adesão, que só aconteceu
efetivamente no século XVI.
Outro fato historicamente interessante foi a origem
do número zero. Não há consenso entre os
historiadores sobre a invenção do zero, atribuída
tanto aos povos da Mesopotâmia quanto aos árabes,
hindus e chineses. Arqueólogos identificaram um
símbolo para esse número em tábuas de escrita
cuneiforme de 300 a.C., feitas na Mesopotâmia,
numa época em que a região era dominada pelos
persas. A invenção do zero aumentou a precisão
de todos os cálculos e trouxe um grande
desenvolvimento para a aritmética e a astronomia.
O sistema de numeração hindu–arábico é o que
utilizamos.
Os números fazem parte efetiva do nosso
cotidiano. Estão em toda parte, nos cercam.
Precisamos deles. Abrimos o jornal e nos
deparamos com notícias repletas de números.
Através deles nos expressamos diariamente.
Você já deve ter ouvido frases como estas...
• “Meu tapete mede 2 metros por 3 metros.”
• “O maior vírus conhecido mede 0,00025 cm.”
• “A parte correspondente a do meu salário é
gasta com despesas mensais fixas.”
• “A catedral fica no marco zero da cidade.”
• “O diâmetro de uma molécula grande é
0,000017 cm.”
• “A temperatura em Nova York era de – 8º Celsius,
enquanto que, no Rio de Janeiro, fazia 30ºC à
sombra.”
• “A cidade Vila Feliz fica no quilômetro 122 da
rodovia João Paulo.”
• “O número encontrado foi 0,3111...”
• “Para calcular o comprimento da circunferência,
basta multiplicar o diâmetro por π, cujo valor é
aproximadamente 3,141592.”
• “O resultado foi 0,333....”
• “Era um número diferente: 0,10110111..”
• “Minha casa fica no número 122 dessa rua.”
• “Pedro conseguiu ser classificado em 1º lugar
no vestibular.“
• “Quando dividi 12 por 33, encontrei como
resultado 0,1212...”
Capítulo III — Convivendo com os números
67
• ”Um freezer congela à temperatura de –18°
Celsius.”
• “Viajamos à velocidade média de 80
quilômetros por hora.”
• “O cano mede de polegadas.”
• ”Um pão de queijo custa R$ 0,80.”
• “A caixa d’água tem 10.000 litros de
capacidade.”
• “Verificamos um resultado de – 0,02%.”
Observe na Figura 1 como os números são escritos
de modos diferentes.
Quantas vezes temos de carregar uma sacola com
várias coisas pesadas e nos perguntamos: Quantos
quilos estarei carregando? Aí começamos a
pensar: São dois quilos e meio de feijão; um quilo
e trezentos de carne; um quilo e meio de farinha e
meio quilo de sal.
Calcule o peso dessa sacola.
Você poderá fazer esse cálculo de vários modos.
• Um deles seria: primeiro, juntar os quilos
inteiros, 2kg de feijão, mais 1kg de carne, mais
1kg de farinha, o que resulta em 4kg.
Depois, juntar os meios quilos: 0,5kg de feijão,
mais 0,5kg de farinha, mais 0,5kg de sal, o que
resulta em 1,5kg.
Juntando os 4kg com 1,5kg, são 5,5kg.
E, por fim, juntar os 300 gramas de carne, o que
resulta em 5kg e 800 gramas, que pode ser escrito
como 5,8kg.
• Outro modo seria pensar que:
dois quilos e meio de feijão são 2,5kg;
um quilo e trezentos de carne são 1,3kg;
um quilo e meio de farinha são 1,5kg;
meio quilo de sal são 0,5kg.
Calculando a soma, teremos:
2, 5
1, 3
1, 5 +
0, 5
5, 8
Veja que, nos dois modos de solução, os números
que usamos foram representados com vírgula.
Esses não são naturais nem inteiros. Podem ser
chamados de racionais e também de números
reais. São conhecidos como decimais e podem
ser escritos em forma de uma fração com
denominador 10, 100, 1.000 etc.
2,5 = 0,48 = 1,245 =
Você vai notar que a escrita de números, às vezes,
usa a vírgula, outras, a forma de fração, como o
. E outras, o sinal negativo, como o -8, que é
um número negativo.
No dia-a-dia, você encontra várias situações
envolvendo esses números. Veja algumas dessas
situações e os problemas propostos. As respostas
que você não encontrar no próprio texto estarão
no final do capítulo.
Vivemos calculando, fazendo estimativas e
pensando em soluções envolvendo números. Por
exemplo: Você está trabalhando na barraca de
refrigerante da quermesse. No início da festa,
havia 400 latas de refrigerantes e você gostaria de
saber quantas vendeu.
Para calcular essa quantidade, é necessário contar
as latas que sobraram e depois encontrar a
diferença entre essa quantidade que sobrou e 400.
Os números usados para resolver esse problema são
chamados de números naturais, mas podem
também ser chamados de inteiros, racionais ou,
ainda, números reais.
Figura 1
Matemática e suas Tecnologias Ensino Médio
68
Observe que o número de casas decimais
(algarismos depois da vírgula) é igual ao número
de zeros do denominador.
As frações surgiram, há muitos anos atrás, com a
necessidade de medir quantidades não inteiras.
Números negativos
Além das frações e dos decimais, o homem, no
decorrer do tempo, precisou de registros para
expressar números menores que zero. Foram
chamados de números negativos, que,
acrescentados ao conjunto dos números naturais,
deram origem a um novo conjunto numérico
chamado de conjunto dos números inteiros.
Atualmente convivemos com situações
envolvendo os números negativos, usados, por
exemplo, para registrar “queda” ou “perda”. As
mais comuns são:
• o saldo bancário devedor;
• as temperaturas abaixo de zero;
• os pontos perdidos no campeonato de futebol.
Ao obtermos a porcentagem de acerto na prova, fica mais fácil percebermos a nota
correspondente. O primeiro aluno ficará com nota 4 ( quatro) e o outro com nota
7,5 (sete e meio).
Usando esses registros, podemos resolver
problemas como:
Numa cidade da Europa, onde no inverno faz
muito frio, o termômetro está marcando
– 8° Celsius, ao mesmo tempo em que, em outra
localidade nesse país, a temperatura é de
– 2° Celsius. Em qual das duas cidades faz mais
frio, na que tem temperatura de – 8° Celsius ou
na que tem – 2° Celsius?
Capítulo III — Convivendo com os números
73
Resolvendo o problema
Antes de discutirmos o problema, vamos lembrar
como fazemos a leitura de um termômetro.
• Um termômetro marca temperaturas abaixo de
zero como negativas e acima de zero como
positivas!
Assim, se está muito frio e a temperatura atingiu 2
graus abaixo de zero, podemos dizer que o
termômetro marcou 2 graus negativos, isto é, a
temperatura local era de –2° Celsius. Se forem 2
graus acima de zero, dizemos, simplesmente,
2° Celsius. (Celsius é a unidade de temperatura
usada no Brasil.)
Você pode observar que, quanto mais abaixo de
zero estiver a temperatura, mais frio estará
fazendo, isto é, – 8º Celsius é uma temperatura
menor do que –2º Celsius.
Essa comparação entre as temperaturas pode ser
escrita em linguagem matemática simbólica. Em
Matemática usamos o sinal > para indicar maior e
o sinal < para indicar menor. Usando esses sinais
podemos escrever:
(-2) > (-8) ou (-8) < (-2).
Escreva você mais alguns números negativos e
compare-os usando os sinais > ou <.
Vejamos mais um problema
envolvendo temperatura
Às 9 horas da manhã, a temperatura estava
agradável, fazia 18ºC. Ao meio dia, passou para
20°C e às três horas da tarde, começou a esfriar
caindo para 17°C. Durante a noite, esfriou muito e,
às 2 horas da madrugada, os termômetros
marcavam –2°C. Às 5 horas da manhã, já estava
marcando – 4°C (C é a abreviação de Celsius e, ao
lermos –2°C, devemos dizer dois graus Celsius
negativos). Encontre a maior variação de
temperatura ocorrida nesse período.
Resolvendo o problema
Use os sinais + ou - para registrar as
temperaturas observadas durante esse período e
encontre a diferença entre a maior e a menor
temperatura.
1. As temperaturas positivas:+18, +20, +17.
2. As temperaturas negativas: –2 e –3.
3. A maior temperatura: + 20.
4. A menor temperatura: – 3.
5. Para calcular a diferença entre -3 e 20, podemos
pensar que:
• de –3 até zero, a diferença é 3.
• de 0 até 20, a diferença é 20.
⇒ Então, a diferença entre –3 e 20 é 23
Figura 9
Matemática e suas Tecnologias Ensino Médio
74
Juntar os dois totais:
+ 2.667,97 – 974,13 = 1.633,84
Números irracionais
Você saberia dizer qual dos dois caminhos a
formiga faz para chegar ao doce?
(a+c) ou b?
O professor Luiz Barco, em sua coluna na revista
Super Interessante nº 147, afirma que até as
formigas escolhem andar pelo maior lado do
triângulo retângulo, em vez de percorrer os
outros dois.
Segundo o prof. Barco, calcular caminhos é uma
das várias aplicações práticas do teorema de
Pitágoras. Usando este teorema, é possível
calcular a menor distância entre dois pontos.
Pitágoras, um filósofo que viveu na Grécia
aproximadamente 500 anos antes de Cristo,
Figura 13
a
b
c
Figura 14
estabeleceu uma relação entre os lados do
triângulo retângulo que ficou conhecida como
“teorema de Pitágoras”.
A descoberta de Pitágoras foi uma revelação para
a Matemática, pois surgiram números para os
quais não é possível extrair a raiz quadrada exata.
O teorema de Pitágoras diz que:
“Em um triângulo retângulo, a soma das
medidas dos quadrados dos catetos é igual
ao quadrado da medida da hipotenusa”.
Capítulo III — Convivendo com os números
81
Veja o que ocorre quando aplicamos o teorema
de Pitágoras em um triângulo retângulo cujos
catetos medem 1m.
Escrevemos:
x
2
= 12
+ 12
x
2
= 1+1
x
2
= 2
x =
Ao calcularmos o valor dessa raiz, com o auxílio
de um computador, encontramos:
=1,4142135623730950488016887242097...
Note que os três pontinhos que aparecem depois
do último algarismo 7 indicam que podemos
continuar calculando essa raiz e ir aumentando
infinitamente o número de casas decimais.
Outro fato importante para ser observado na
representação decimal desse número é que não
acontece com ele o mesmo que com outros
números racionais que também têm infinitas casas
decimais, como, por exemplo, os números
1,33333..., 52,15234234234234... Nesses casos, a
partir de um determinado algarismo, há, na parte
decimal, regularidade na repetição de algarismos.
Veja que para essa regularidade não ocorre.
Números como o são chamados de irracionais
porque não é possível escrevê-los na forma de
uma razão, isto é, na forma fracionária com
numerador e denominador inteiros. Existem
muitos números irracionais. Veja mais alguns:
; ; 0,10101101111... e o conhecido π, que
nos permite calcular a área do círculo e o
perímetro da circunferência.
Você viu, no decorrer desse capítulo que o
conhecimento dos números e suas operações
pode ajudá-lo em diferentes situações cotidianas.
Existem, ainda, outras situações reais nas quais o
conhecimento dos números irracionais pode
ajudá-lo e a toda sua comunidade.
Os mutirões entre vizinhos, para a construção da
casa própria, ocorrem em grande número em
diferentes regiões do país.
Veja uma possibilidade de usar seu conhecimento
dos números para resolver problemas que podem
aparecer em construções.
Figura 16
Como você faria para calcular aproximadamente a
medida da viga lateral da estrutura de um telhado
como o da figura acima?
Resolvendo o problema
Você deve ter encontrado o valor para x. Para
obter o valor aproximado, você pode usar uma
calculadora ou então considerar que:
como 5 é maior que 4, então deve ser maior
que ; mas é igual a 2,
como 5 é menor que 9, então deve ser menor
que ; mas é igual a 3,
então é um número que está entre 2 e 3.
Como 5 está mais próximo de 4 do que de 9,
então deve estar mais próximo de 2 do que
de 3.
Assim, multiplique 2,1 por 2,1 e, depois,
multiplique 2,2 por 2,2; experimente também
multiplicar 2,3 por 2,3.
Qual dos resultados que você obteve mais se
aproxima de 5?
Se você achar que é o produto de 2,2 por 2,2,
então poderá dizer que é aproximadamente igual
a 2,2.
Isso quer dizer que a medida da viga é de
aproximadamente 2,2 metros, que é o mínimo
necessário. Porém, como há alguma perda em
cortes, você deve considerar alguns centímetros a
mais na hora da compra do material.
ESTUDE AS IMAGENS E FÓRMULAS EM:
http://download.inep.gov.br/educacao_basica/encceja/material_estudo/livro_estudante/encceja_matematica_ens_medio.pdf
ESTUDE CADA TEMA DA MÁTEMÁTICA/ REVISÃO EM:
http://www.gabarite.com.br/material-concurso/64-apostila-completa-de-ensino-medio-para-concursos-gratis
terça-feira, 21 de novembro de 2017
Assinar:
Postar comentários (Atom)
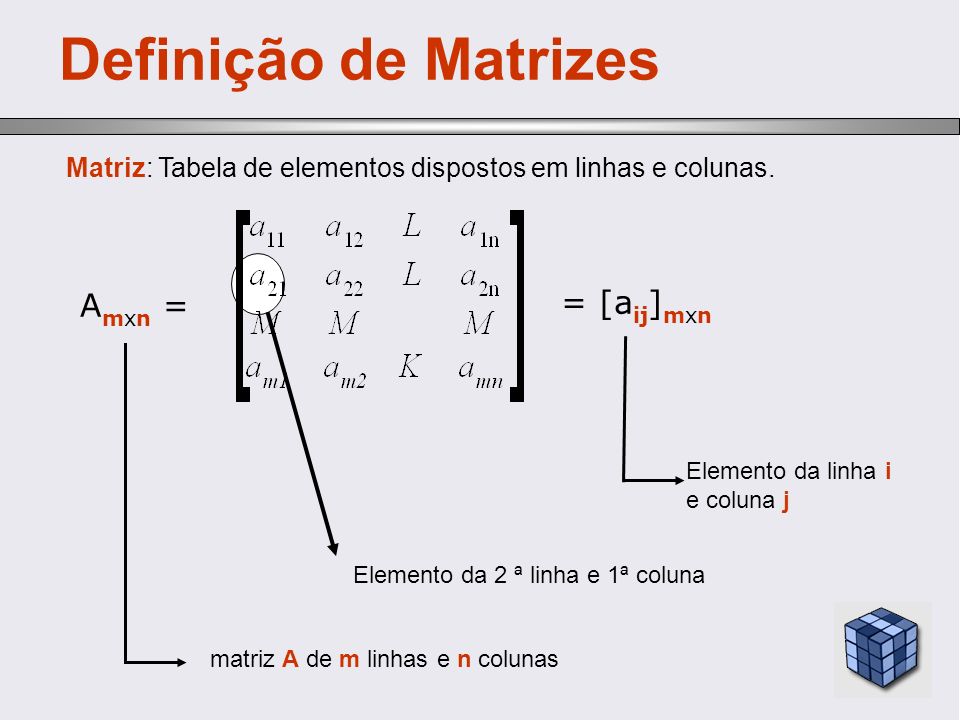
Matemática - Matrizes
Análise Combinatória: Números Complexos: Polinômios: Estatística: (analise dos gráficos e tabelas e responder ás perguntas...
-
A Matemática e o dia-a-dia Apesar de o homem não ter registrado o que fazia e pensava no início de sua história, ele precisava resolver...
-
Matemática e suas Tecnologias Livro do Estudante Ensino Médio A Matemática: uma construção da humanidade A Matemática e o dia-a-dia As con...
-
Ciências Humanas e suas Tecnologias Livro do Estudante Ensino Médio TEMAS/ DESTAQUES PARA A PROVA: Cultura, memória e identidade: um car...
Nenhum comentário:
Postar um comentário